时间：2021年6月17日，15:00-18:00
地点：X2511
主持人：周正春教授
报告一（15:00-16:00）
题目：Further results on optimal ternary cyclic codes
报告人：查正邦 教授
摘要：Let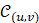 
denote the ternary cyclic code with two nonzeros 
and , where is a generator of and . In this paper, we present a sufficient condition such that is an optimal ternary cyclic code. Based on this condition, we get several classes of optimal ternary cyclic codes by choosing the proper and . Moreover, we show that and have the same optimality.
报告人简介：查正邦，洛阳师范学院数学科学学院教授，硕士生导师，湖南大学理学博士，中科院信息工程研究所博士后。承担近世代数、初等数论、现代密码学和高等数学等课程，主编“十一五”国家级规划教材2部，获全国高校数学微课程教学设计赛河南赛区二等奖2项、河南省教育厅师德主题教育征文二等奖1项，先后被评为“河南省高校优秀共产党员”、“洛阳师范学院优秀教师”、“洛阳师范学院文明教工”和“洛阳师范学院大学生最喜爱的老师”。主要研究领域为代数编码、密码函数，先后在《IEEE Trans. Inf. Theory》、《Journal of Algebra》、《中国科学：数学》等国内外学术期刊上发表论文三十余篇，其中SCI收录26篇，EI收录2篇，获河南省自然科学优秀学术论文奖一等奖1项、二等奖5项。出版学术专著1部，主持国家自然科学基金面上项目2项、青年基金项目1项，主持完成国家重点实验室开放课题、中国博士后科学基金等省部级项目4项，先后获得“河南省学术技术带头人”、“河南省高层次(C类)人才”、“河南省高校青年骨干教师”、“河南省高校科技创新人才”、“洛阳市优秀专家”等荣誉称号。他是中国密码学会和中国数学会高级会员、河南省青年科技工作者协会会员，多次担任国家自然科学基金通讯评审专家。
报告二（16:00-17:00）
题目：互不相关码研究进展
报告人：王琦 研究员
摘要：由于近十多年来被应用于解决帧同步问题，尤其是在DNA存储系统中作为地址标识码实现随机存取关键特性，互不相关码受到越来越多的关注。在本报告中，我们将介绍互不相关码的背景、理论界、构造以及相关最新进展。
报告人简介：王琦，南方科技大学工学院计算机科学与工程系研究员。他于2007年在中国科学技术大学信息安全专业获得学士学位，于2011年在香港科技大学计算机科学与工程系获得博士学位。他曾受德国洪堡基金会遴选于德国马格德堡大学威廉希尔亚洲公司进行博士后研究。他的主要研究方向包括纠错编码、组合设计、密码学及应用，他在IEEE TIT、DCC等相关领域国际知名期刊和会议已经在发表了三十余篇SCI/EI学术论文。他曾主持结题国家自然科学基金面上项目、青年项目、科技部重点研发计划子项目等，参与国家自然科学基金重点项目等。
报告三 （17:00-18:00）
题目 Shortened linear codes from APN and PN functions
报告人：唐春明 研究员
摘要：Linear codes generated by component functions of perfect nonlinear (PN) and almost perfect nonlinear (APN) functions and the first-order Reed-Muller codes have been an object of intensive study in coding theory. In this talk we will investigate some binary shortened codes of two families of linear codes from APN functions and some p-ary shortened codes associated with PN functions. The weight distributions of these shortened codes and the parameters of their duals are determined. The parameters of these binary codes and p-ary codes are flexible. Many of the codes presented in this talk are optimal or almost optimal. The results show that the shortening technique is very promising for constructing good codes.
报告人简介：唐春明，西华师范大学数学与信息学院副院长，硕士研究生导师。2012年毕业于北京大学数学科学学院，获博士学位，并先后在巴黎第八大学和香港科技大学从事博士后研究工作。主要研究包括密码、编码及其相关的数学理论，先后主持国家自然科学基金青年项目和面上项目各一项，发表研究论文 60 余篇，其中 EI、SCI 检索论文 50 余篇，代表性成果发表在国内外重要学术期刊《IEEE Transactions on Information Theory》《Finite Fields and Their Applications》《Designs, Codes and Cryptography》《Science China》和《China Communications》等。现为《IEEE Transactions on Information Theory》、《Designs, Codes and Cryptography》、《IEEE Communications Letters》等SCI、EI期刊审稿人，同时兼任三个国际期刊的编委。
